728x90
Quick Sort는 분할 정복 방법을 통해 주어진 배열을 정렬한다.
불안정 정렬, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬!
Merge Sort와 달리 Quick Sort는 배열을 비 균등하게 분할
💡 분할 정복 방법이란? 문제를 작은 2개의 문제로 분할하고 각각을 해결하고 결과를 모아 원래의 문제를 해결하는 방법
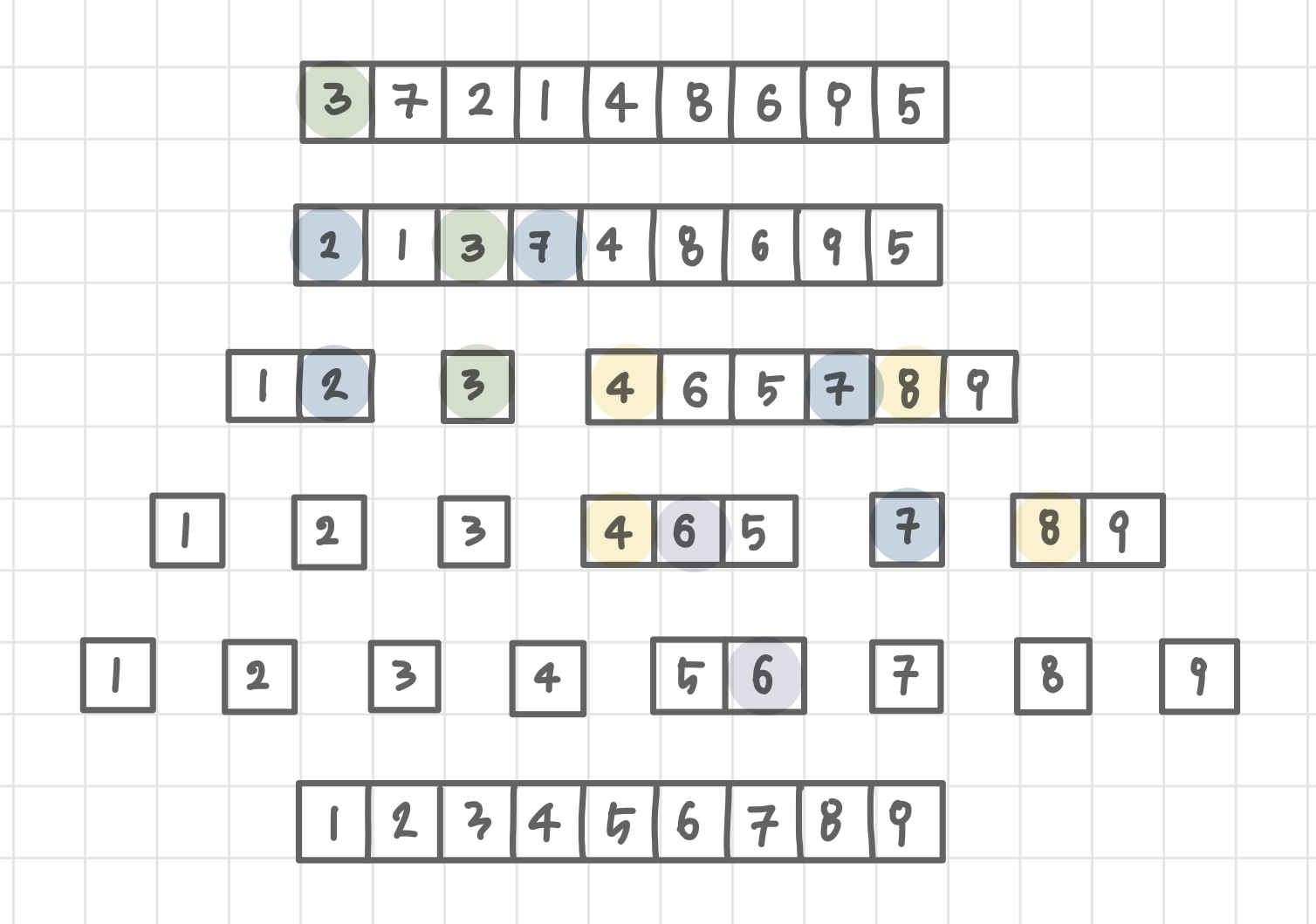
과정
- 배열 가운데에서 하나의 원소를 고른다 (pivot)
- pivot 앞은 pivot보다 작은 모든 원소들이 오고, 뒤는 pivot보다 큰 모든 원소들이 오도록 한다 (Divide)
- pivot을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬 (부분 리스트 속에서도 pivot 정해서 반복)
- 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복 (리스트 크기 0 혹은 1)
→ 재귀 호출이 한 번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해 지므로, 끝남을 보장한다.

코드
void quickSort(int arr[], int l, int r){
if(l>=r) return;
int pivot = partition();
quickSort(arr, l, pivot-1);
quickSort(arr, pivot+1, r);
}
void partition(int arr[], int l, int r){
int pivot = arr[l];
int i = l, j = r;
while(i<j){
while(pivot < arr[j]) j--;
while(i<j && pivot >= arr[i]) i++;
swap(arr, i, j);
}
arr[l] = arr[i];
arr[i] = pivot;
return i;
}시간 복잡도
- 최선/평균의 경우: O(nlogn)
- 비교 횟수 : logn→ O(nlogn)
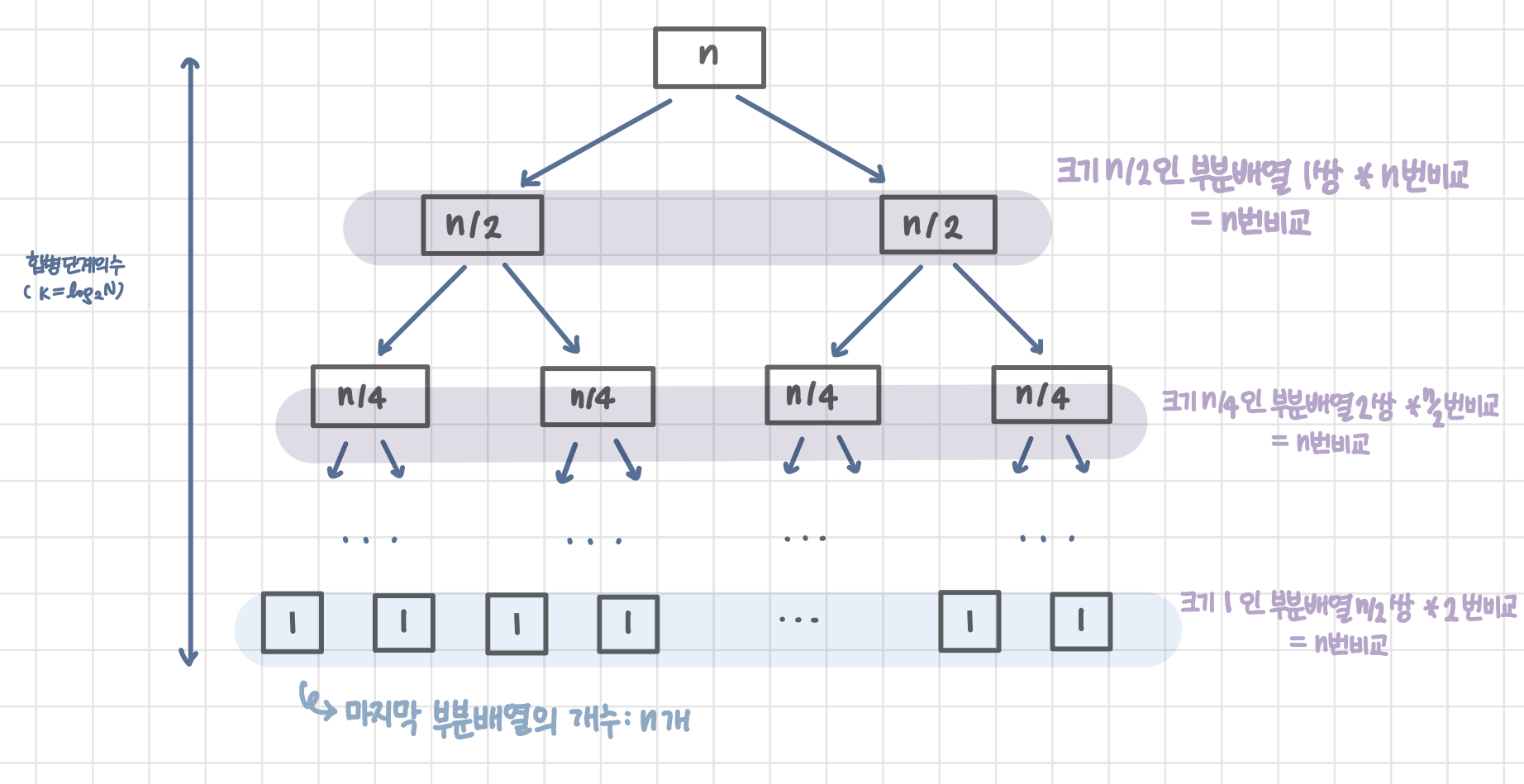
- 전체 리스트의 대부분의 레코드를 비교해야하므로 평균 n번의 비교가 이루어진다.
- 비교 횟수 : logn→ O(nlogn)
- 최악의 경우: O(n^2)
- 순환호출의 깊이가 n, 비교 연산 n
- → O(n^2)
- 정렬하고자 하는 배열이 이미 오름차순 혹은 내림차순으로 정렬되어 있는 경우
장점
- 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라 한번 결정된 피벗들은 추후 연산에서 제외되기 때문에 시간 복잡도가 O(nlogn)인 다른 정렬 알고리즘과 비교해도 가장 빠르다!
- 다른 메모리 공간 필요 X
단점
- 불안정 정렬
- 정렬된 배열에 대해서는 Quick Sort의 불균형 분할에 의해 오히려 시간이 오래 걸린다.
💡공부 및 기록용 블로그이므로 오류가 있을 수 있습니다.💡
만약 문제에 오류나 오타가 있다면 댓글로 알려주세요➿
언제나 환영합니다. 감사합니다. 화이팅!
참고: https://gmlwjd9405.github.io/2018/05/06/algorithm-quick-sort.html
728x90
'알고리즘' 카테고리의 다른 글
| [알고리즘] 기수 정렬(Radix Sort) (0) | 2022.02.14 |
|---|---|
| [알고리즘] 힙 정렬(Heap Sort) (0) | 2022.02.13 |
| [알고리즘] 합병 정렬(Merge Sort) (0) | 2022.02.12 |
| [알고리즘] 삽입 정렬(Insertion Sort) (0) | 2022.02.12 |
| [알고리즘] 선택 정렬(Selection Sort) (0) | 2022.02.12 |