알고리즘
[알고리즘] 기수 정렬(Radix Sort)
녕이
2022. 2. 14. 17:52
728x90
데이터를 구성하는 기본 요소(Radix)를 이용해 정렬을 진행하는 방식
낮은 자릿수부터 비교해 정렬하는 알고리즘 (LSD)
비교 연산을 하지 않으며 정렬 속도가 빠르지만 데이터 전체 크기에 기수 테이블의 크기만 한 메모리 추가 필요
입력 데이터의 최댓값에 따라서 couting sort의 비효율성을 개선하기 위해, radix sort를 사용 자릿수의 값 별로 정렬하기 때문에 나올 수 있는 값의 최대 사이즈는 9 (0~9)
과정
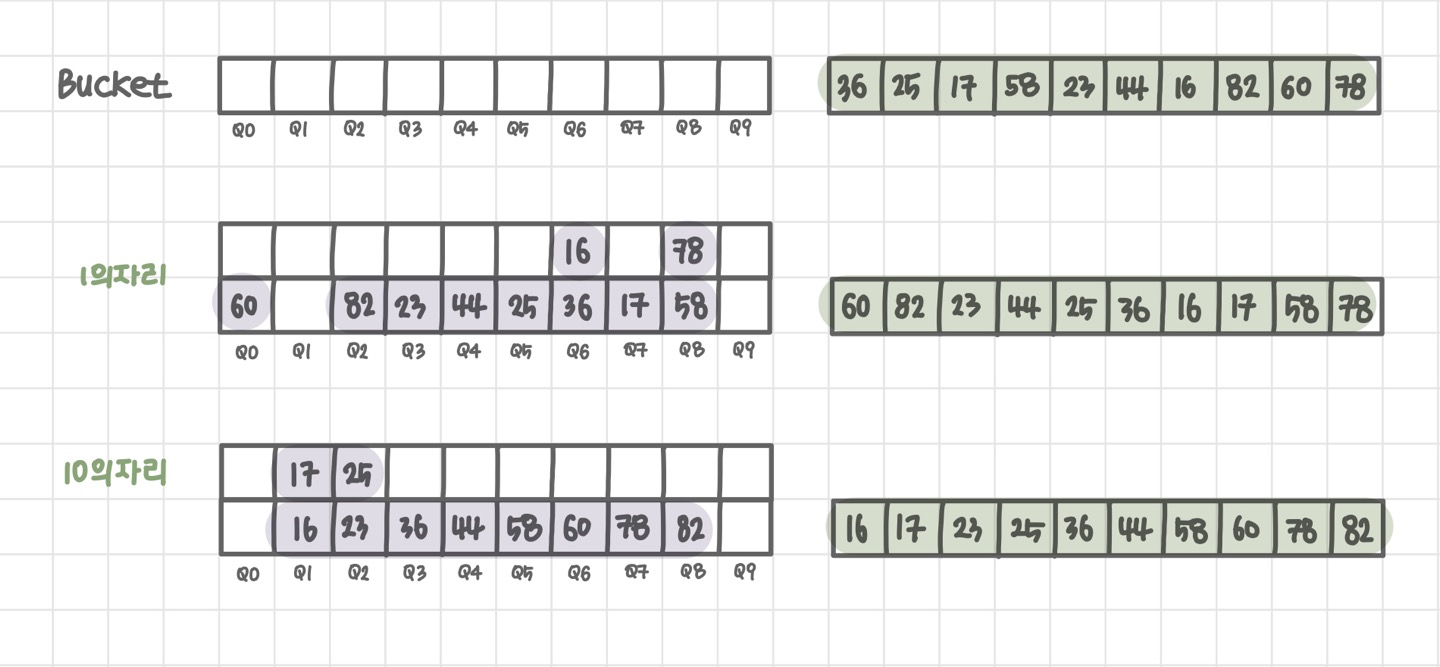
- 0~9 까지의 Bucket(Queue 배열) 준비
- 모든 데이터에 대해 가장 낮은 자릿수에 해당하는 Bucket에 차례대로 데이터 삽입
- 0부터 차례대로 Bucket에서 데이터를 다시 가져온다
- 가장 높은 자릿수를 기준으로 자릿수를 높여가며 2번, 3번 과정을 반복
코드(c++)
#include <iostream>
#include <queue>
#include <algorithm>
#define N 10
using namespace std;
queue<int> bucket[N];
int powed = 1;
int ind;
//가장 큰 자릿수 찾기
int getMax(int arr[], int n){
int maxValue = *max_element(arr, arr+n); //MAX VALUE
int a = maxValue, maxCount = 0;
do{
a /= 10;
maxCount++;
}while(a != 0);
return maxCount;
}
void radixSort(int arr[], int n){
int maxNum = getMax(arr, n); //가장 큰 자릿수
for(int i=0; i<maxNum; i++){
//자릿수에 맞는 index bucket에 넣기
for(int j=0; j<n; j++){
bucket[(arr[j]/powed)%10].push(arr[j]);
}
//임시 배열에 넣기
for(int k=0; k<10; k++){
while(!bucket[k].empty()){
arr[ind++] = bucket[k].front();
bucket[k].pop();
}
}
powed *= 10;
ind = 0;
}
}
int main(){
int arr[] = {170, 45, 75, 90, 802, 24, 2, 66};
// int arr[] = {36, 25, 17, 55, 44, 23};
// int arr[] = {36, 25, 17, 58, 23, 44, 16, 82, 60, 78};
int n = sizeof(arr) / sizeof(arr[0]); // 좋은 습관
radixSort(arr, n);
for (int i = 0; i < n; i++){
cout << arr[i] << " ";
}
return 0;
}
시간 복잡도 O(d * n + b))
→ d: 정렬한 숫자의 자릿수, b: 10
(counting sort의 경우, O(n+k)로 배열의 최댓값 k에 영향받는다)
장점
- 문자열, 정수 정렬 가능
단점
- 중간결과를 저장할 bucket 공간이 필요
- 자릿수가 없는 것은 정렬할 수 없음(부동 소수점)
Q) 왜 낮은 자리수부터 정렬할까?
MSD와 LSD를 비교해보면
MSD는 가장 큰 자리수부터 Couting Sort 하는 것을 의미하고, LSD는 가장 낮은 자릿수부터 Counting Sort 하는 것을 의미한다.
- LSD의 경우 1600000과 1을 비교할 때, Digit의 개수만큼 따져야 하는 단점 MDS의 경우, 마지막 자릿수까지 확인할 필요가 없다!
- LSD는 중간에 정렬 결과를 알 수 없다. MSD는 중간에 중요 숫자를 알 수 있다 → 시간 줄일 수 있다.→ 확인하는 과정이 필요하므로 메모리 추가 사용
- LSD는 알고리즘 일관 → Radix Sort는 주로 LSD MSD는 일관되지 못함
- LSD는 자릿수가 정해진 경우, 좀 더 빠를 수 있다.
💡공부 및 기록용 블로그이므로 오류가 있을 수 있습니다.💡
만약 문제에 오류나 오타가 있다면 댓글로 알려주세요➿
언제나 환영합니다. 감사합니다. 화이팅!
[참고]
https://lktprogrammer.tistory.com/48
https://gyoogle.dev/blog/algorithm/Radix%20Sort.html
728x90